前言
本人阅读顺序依照 如何从零开始学习凸优化?:
- 先读 Convex Optimization: Algorithms and Complexity
- 再读 Optimization Methods for Large-Scale Machine Learning。
本博文仅作为快速反馈的工具,以及每日的笔记所存在。配合这两篇文章一起阅读更佳。加起来一共二百三十几页,也就是说,每天读十页,三周多一点就能跟到较前沿的位置。
前五天的笔记记录在此。以天数进行分段。
先上一张本书中的 Summary Table:
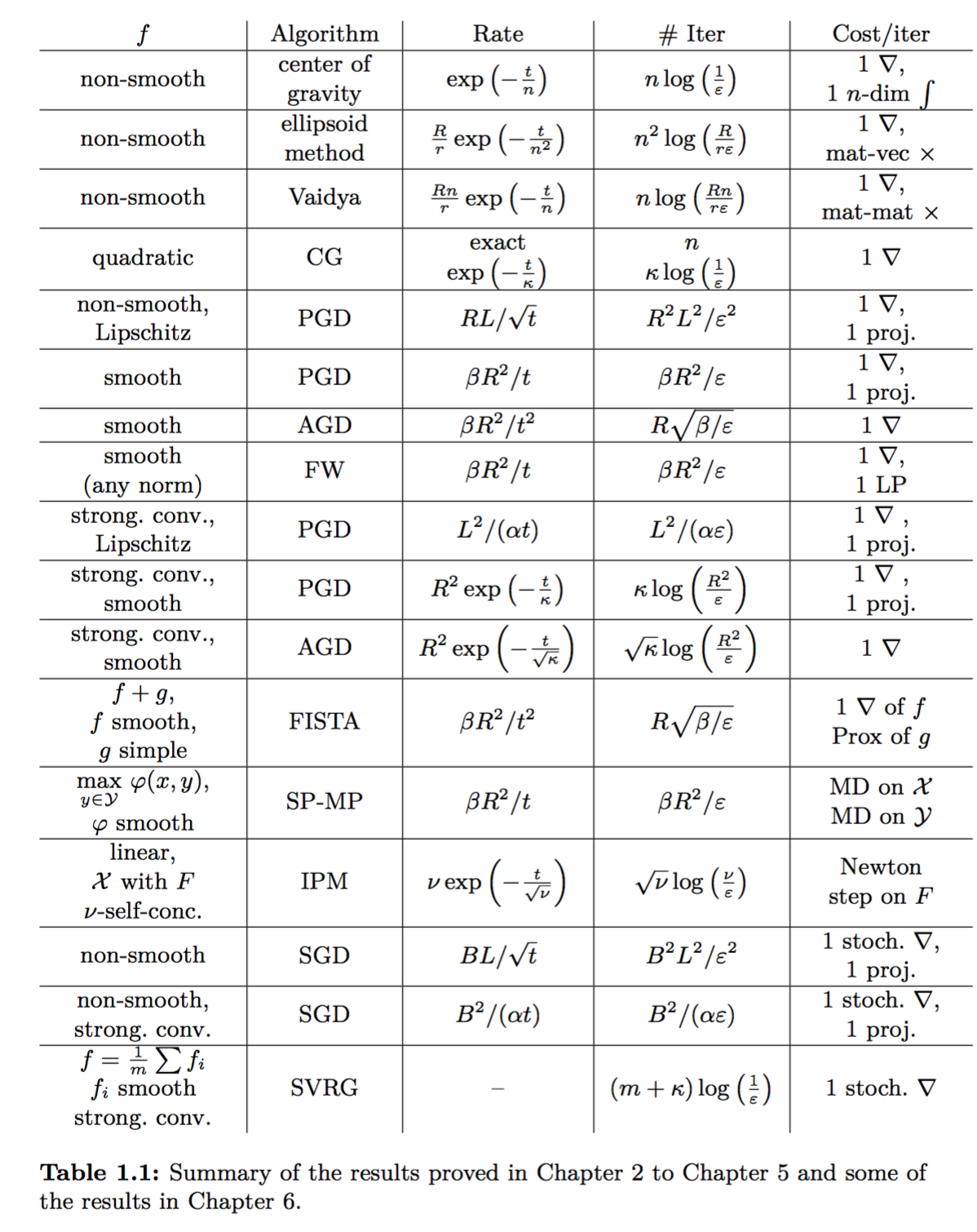
第一天
什么是凸集
有个集合,对于该集合内的任意两点之间连线,若该线上的任意点仍然落于该集合内,则该集合为凸集。
超平面分离定理
该定理说:对于凸集边界上的某个点,必然能够找到某个方向,从该方向上看,该边界上的点挡在凸集的最前面。
Subgradient
定义可参考 Stanford slides。
有一个很好的性质:X 为凸集下,f 为凸的充要条件:X 内的任意点均存在 subgradient。X 为 f 的 定义域。
引入 Subgradient 的意义见下一段。此外也有文章说是可以用来解决不可导凸函数的优化的。
凸优化的意义
有时候我也不懂凸优化的意义何在。不是只要 SGD 就够了吗?顶多加上一些动量方法。这里是作者给出的解释:
- 凸集 + 凸函数时,局部极小点与全局极小点等价。
- 许多非凸的优化情况能够转化为凸优化问题:SVM,岭回归,逻辑回归,LASSO,矩阵补全……
作者还给出了一个很有趣的观点:凸优化中的函数都呈现出了从 local 到 global 的 phenomenon。某点的梯度信息给出了当前点附近的局部信息,而它的 Subgradient 则给出了一组整个函数的近似线性的 lower bound(我理解为直线绕该点组成的圆锥)。凸优化的很多算法,都利用了这个性质。
小结
超平面分离定理还挺形象的,学到了为什么要做凸优化,第一天,过!
第二天
黑盒模型
黑盒模型假设:已知函数定义域,给定无限的计算资源,但不知道 objective function,需要通过 access oracle 才能够知道。
黑盒模型关注于,需要通过多少次 access oracle,才能够到达离函数最优值只差 $\epsilon$ 的解。这里的次数,称之为 oracle complexity.
为什么要引入黑盒模型?引入黑盒模型的好处在于,它抽象化了 objective function 的形式,一定程度地泛化了优化算法的性能结论。我们也进一步地泛化黑盒模型,比如将函数定义域的信息也作为 oracle 封装,每次都要咨询 oracle,某点是否在定义域内。在这个情况下,要考虑的要素就有了两个了:定义域查询的复杂度、以及目标函数查询的复杂度。
当然,如果引入 objective function 的详细信息,那么算法可能会在黑盒模型得到的算法的基础上,进一步地优化,比如说 Interior Point Methods。
给定 x,有两种目标函数的 oracle:
- zeroth order oracle:
- 返回 f(x)
- first order oracle:
- 返回 x 处的 subgradient
Convex Optimization in Finite Dimension
此处的 Finite Dimension,指的是定义域的空间维度是有限的。此类方法的复杂度与维度是有关的。需要注意:
An interesting feature of the methods discussed here is that they only need a separation oracle for the constraint set X . In the literature such algorithms are often referred to as cutting plane methods.
具体来说,Cutting Plane Methods 可用来识别某个集合是否为空,或等价地,寻找存在于某集合内的一个任意点(即 feasibility problem)。可以参考 Boyd 的 Localization and Cutting-Plane Methods.
重心方法:Center of Gravity Method
假设你的新网友让你猜他的岁数。你不知道,于是将 100 对半,问是否大于 50。我们知道,这样对半的方法叫做二叉树。
重心方法很类似。你在地球上,你想找出太阳的中心,你有一件无坚不摧、冬暖夏凉、自制空气的衣服。你该怎么做?穿上衣服,把自己发射到外太空,让自己漂浮,从太阳南边被吸引,然后飞过去,到达太阳北边,再飞回来到达南边。如此往复,像蹦极一样,总有一天因为能量耗散光而最终到达太阳的重心。
如下图所示:

当然书中略有不同,梯度变为了 subgradient 的任意一元素。
重心方法的渐进收敛证明思路
简单说下,证明思路基于两个事实:
- 最优点不会从当前的集合里删掉。
- 集合在逐步缩小。
小结
说实话,重心模型确实很有意思,也很直观。黑盒模型的引入,也使得证明很干净,不用考虑各种目标函数。第二天,完!
第三天
Ellipsoid Method
如下图。每张图中,被虚线平分的是当前的椭圆;不被平分的是下一步形成的椭圆。
当前椭圆中心属于 X 时,虚线的含义是 X 处的某个 subgradient 形成的超平面;当前椭圆中心不属于 X 时,虚线的含义是能够分割在 X 与 X 以外空间之间切下一刀的超平面。在此图中,超平面的法向量就是当前椭圆中心在目标函数上的梯度;在书中,梯度改为了 subgradient。
每次迭代,都会生成一个新的椭圆,新的椭圆包含了原有椭圆的的一半。原有椭圆的哪一半?与超平面的法向量相反方向的那一半,因为这一半中必然含有最优解(证明略)。
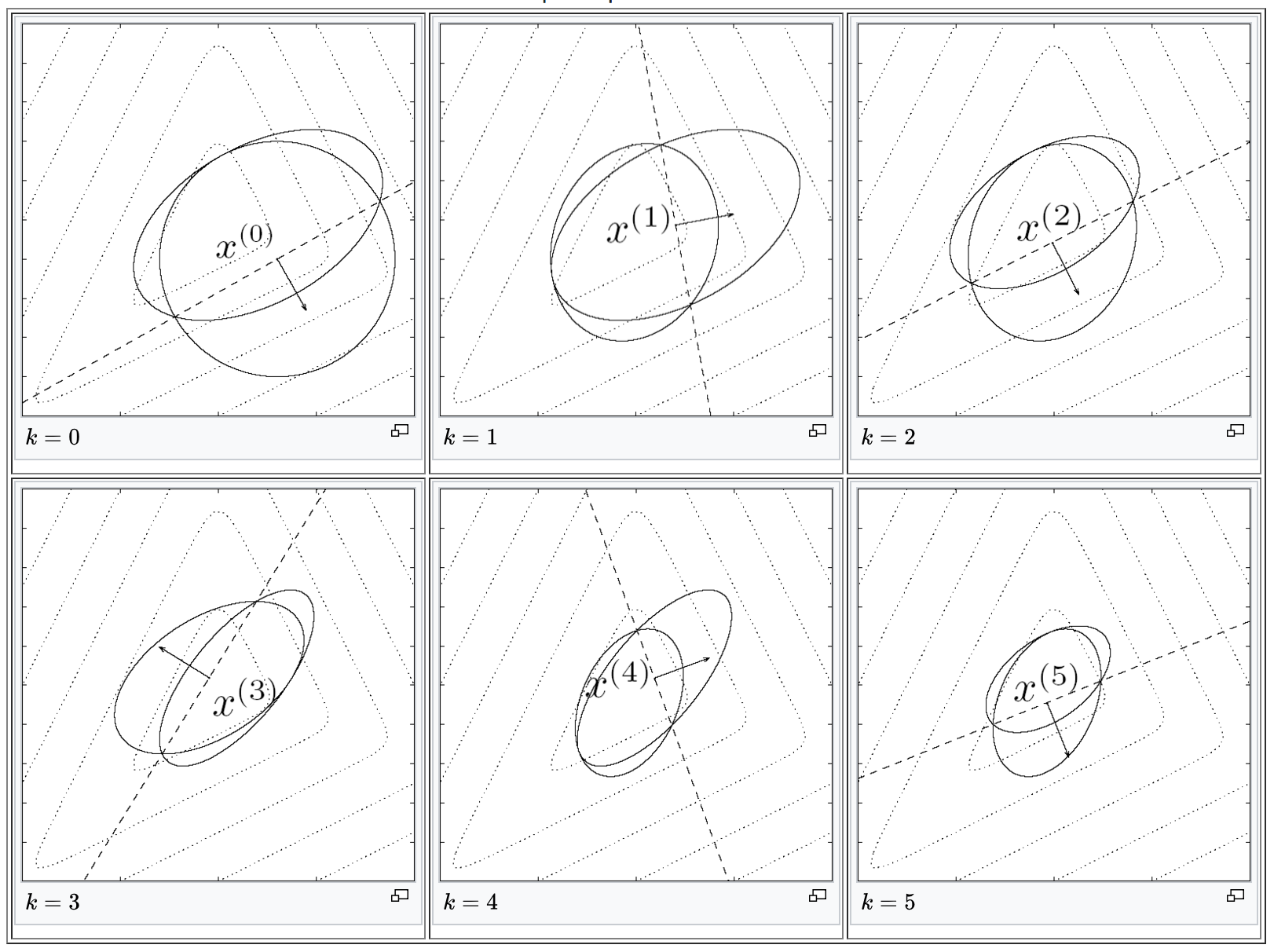
原图出自 Boyd 的 Slides.
证明方式仍然与 Center of Gravity Method 一致:
- 最优点不会从当前的集合里删掉。
- 集合在逐步缩小。
尽管 Ellipsoid Method 的 oracle complexity 比 Center of Gravity Method 的 oracle complexity 差很多,但是 Center of Gravity Method 很棘手(这里我的理解是,算重心很难)。然而,Ellipsoid Method 并不是很常用,因为它规模缩小的方法是 fixed 的,难以更进一步地榨干价值。
接下来的这节 Vaidya’s cutting plane method 是讲 feasibility problem 的,直接跳。
Conjugate Gradient
为什么共轭梯度法会放在这一章里面?因为这个方法的 oracle complexity 是跟维度有关的。空间有多少维,就得迭代多少次。
共轭梯度可用来解线性系统,即 $Ax=b$. 这等价于优化 $f(x)=\frac{1}{2}x^\top Ax-b^\top x$,其中,$A$ 是正定矩阵。
具体来说,共轭的含义是:给定一组正交基集合,顺序地沿着集合中向量的方向,最小化目标函数。
进一步地,怎么找到这一组正交基呢?正常的情况下,直接沿着坐标轴方向即可。但在书中的黑盒情况下,我们只能知道某点的梯度,而不能求沿着某坐标轴的偏微分。其实方法很简单:当前的优化方向会产生一个超平面,那么下一次的优化方向,取当前点的梯度在该超平面上的投影即可。
这里的正交,指的是 $\langle p_i, p_j\rangle_A=p_iAp_j=0$。这样做的好处,在于可以导出 $\langle \nabla f(x_{t+1}), p_i\rangle = 0,$ $\forall 0\leq i \leq t$ 的结论,即一旦在某方向上优化,则最优点必然落在该方向的优化点的超平面内。共轭方法,就这样不断地减少需要优化的维度,直到迭代 $n$ 次。
令人惊喜的是,书中得出了共轭梯度方法的迭代次数在一阶方法,即只用到了函数的一阶导数的信息的方法中,是 optimal 的结论。此外,该方法可以泛化到非二次的凸函数上。这在下一章会有进一步的解释。
小结
共轭梯度法,目前看来,是有局限的,只能够解上述的二次型凸函数,且是简单的线性系统的等价函数。椭圆方法,比起重心方法来说,更加容易实现,因为不需要积分算重心(这很难);然而也榨不出进一步的价值(因为收缩方法是固定的)。第三天,完!
第四天
Gradient Descend Method
终于来到了第三章,dimension-free convex method,很容易理解,这些方法的 oracle complexity 是和定义域的维度不相关的。
Projected Subgradient Descend
终于讲到投影梯度下降了。之前经常在解稀疏方程的时候看到这个方法。我们之所以用投影,是因为有时候迭代得到的下一个点并不属于定义域,因此需要进行转化,将得到的下一个最优点投影到定义域内:
$$y_t = x_t - \eta g_t, \text{ where } g_t \in \partial f(x_t)$$
$$x_{t+1} = \Pi_X(y_{t+1})$$
$$\Pi_{X}(x) = \arg\min_{y\in X}||x-y||$$
其中$X$为定义域,$y$为实际得到的下一个迭代点。
之所以用 $\Pi$ 这个投影函数的原因,在于其可以导出 $||y_{s+1}-x^\ast|| \geq ||x_{s+1}-x^\ast||$ 的结论,从而能够证明最优解的收敛。具体可参见 Lemma 3.1,我把它称之为钝角定理。
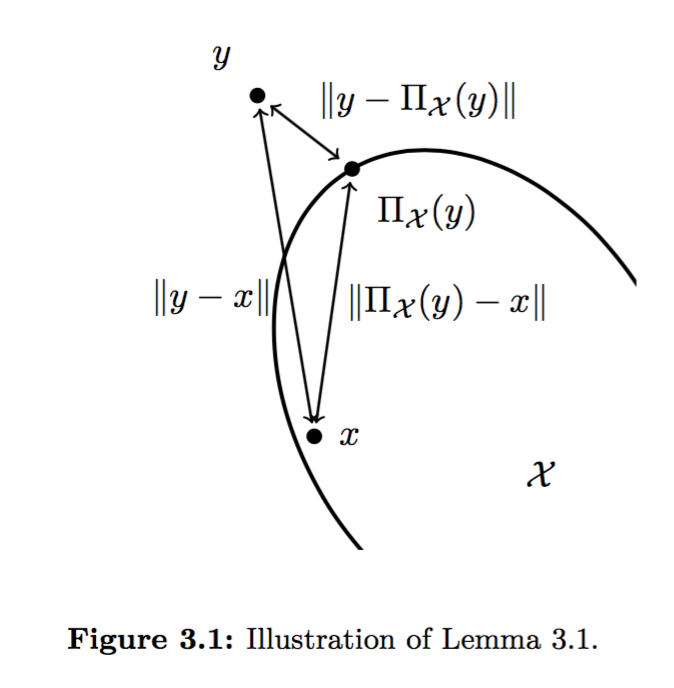
此处 $x$ 为定义域中任意一个元素。由于定义域是凸集,则 $y-\Pi_X(y)$ 与 $x-\Pi_X(y)$ 必形成直角或钝角,则它们点乘的结果必小于等于0,同时也能够得到上述证明最优解的收敛的引理。
选择 Learning Rate
在上述的投影梯度下降算法中,有一个常数,$\eta$,我们还没有确定下来。怎么办?
作者引入了 Liptschitz 连续性。具体来说,若函数是 $L$-Liptschitz 连续的,即 $||f(x)-f(y)||\leq L||x-y||$,那么如果使 $\eta = \frac{R}{L\sqrt{t}}$,则函数的 oracle complexity 为 $\Theta(\frac{1}{\epsilon^2})$,其中 $t$ 为总迭代步数,$R$ 为定义域半径。
比起之前提到的重心方法,椭圆方法来说,如果以 $\epsilon$ 为变量,投影梯度下降方法要慢上很多,然而,在很高维的情况下,由于 Projected Subgradient Descend 是 dimension-free 的(可以分布式计算各维的梯度分量),因此还是使用投影梯度下降方法,它优化的余地比较大。
另外一个值得注意的地方,很多时候我们是不知道一共要迭代多少次,即 $t$ 的实际大小的。因此可以使用 $\eta = \frac{R}{L\sqrt{s}}$ 作为代替,$s$ 为当前已迭代的次数。
光滑函数的梯度下降
从这篇 monograph 的一开始的那张表,我们便可以窥见作者的思路:榨。不断地讨论函数的性质,从而得出更优秀的收敛上界。
引入 $\beta$-smooth:(后记:这里的 $\beta$ 与后面的 $\alpha$-strongly convex 遥相呼应,组成了条件数的定义)。
We say that a continuously differentiable function $f$ is $\beta$-smooth if the gradient $\nabla f$ is $\beta$-Lipschitz, that is $$||\nabla f(x) - \nabla f(y)|| \leq \beta ||x-y||.$$
值得一提的是,如果$f$的导数仍然可以可导,那么 $\beta$ 就是其 Hessian 矩阵特征值的上界。
为什么要引入光滑条件?它能够进一步地缩小收敛所需的步数。如果我们使 $\eta = \frac{1}{\beta}$,那么 $t$ 步之后和最优目标函数值的差距将从之前的 $\Theta(\frac{1}{\sqrt{t}})$ 到 $\Theta(\frac{1}{t})$ (见 Theorem 3.2 和 Theorem 3.7)!
Theorem 3.2. The projected subgradient descent method with $\eta = \frac{R}{L\sqrt{t}}$ satisfies $$f(\frac{1}{t} \sum _{s=1}^t x_s)-f(x^\ast) \leq \frac{RL}{\sqrt{t}}.$$
Theorem 3.7. Let $f$ be convex and $\beta$-smooth on $\mathbb{R}^n$. Then the projected gradient descent with $ \eta = \frac{1}{\beta}$ satisfies $$f(x_t)-f(x^\ast)\leq \frac{3\beta ||x_1-x^\ast||^2+f(x_1)-f(x^\ast)}{t}.$$
总结
终于进入了正轨。第四天,结束!
第五天
Conditional Gradient Descend
Conditional Gradient Descened 迭代步骤:
$$y_t \in \arg\min_{y\in X}\nabla f(x_t)^\top y$$
$$x_{t+1} = (1-\gamma_t)x_t + \gamma_t y_t$$
$x_t$ 为第 $t$ 步时的优化点,$\gamma_t$ 是一个参数。它的收敛上界为 $\Theta(\frac{2\beta R^2}{t+1})$.
为什么要用 Conditional Gradient Descend,它的好处是什么?
- Dimension-free. 这个性质是本章一开始就提到的,不再复述。
- Projecion-free. 有没有看到,在迭代过程中,没有出现映射函数,但每次的迭代点都处于定义域以内。Projected Subgradient Method 的一个难受的地方就在于对于 $\Pi_X(\cdot)$ 的运算;而 Conditional Gradient Descend 直接使用凸集内两个点的线性组合解决了这个问题。
- Norm-free. 这个性质很好地将光滑性从欧几里得度量扩展到了任意度量。换句话说,只要某函数支持某度量(可以不是欧几里得度量)下的光滑性,那么它就可以使用 Conditional Gradient Descend 得到的结论。
Sparse Iterates. 如果凸集是一个高维的多边体的话,很容易就能想到,$x_{t}$ 是最多 $t$ 个顶点的线性组合。更重要的是,如果每个顶点只有一个分量不为 0 的话,那么 $x_{t}$ 顶多只有 $t$ 个分量不为 0!
Thanks to the dimension-free rate of convergence one is usu- ally interested in the regime where $t \ll n$, and thus we see that the iterates of conditional gradient descent are very sparse in their vertex representation.
书中举了个使用 Conditional Gradient Descend 解决 LASSO 问题的例子,可以在 3.11 式中看到,在求 $x_t$ 时,由于 $x_t$ 最多由 $t$ 个顶点组成,而这些顶点在 LASSO 的约束下各自最多有一个非零分量,因此时间从 $\Omega(N)$ 变为了 $O(t)$,从而大大减少了 time complexity!

总结
解多边形式的凸集下的凸问题,Conditional Gradient Descend 能大大减少计算的复杂度。第五天,结束!