前言
上一篇 太长了,建个新的。
这几天看得越来越慢,结论也觉得推得很慢,每步都看得仔细。任务渐渐完不成,就很慌张。后来发现没必要。抓大放小,把整体思路和文章的比较重要的结论写下来就行了。
第六天
Strong Convexity
强凸性和光滑是一对 dual conception。当且仅当 $f-\frac{\alpha}{2}||x||^2$ 为凸函数时,$f$ 才为 $\alpha$-strongly convex function.
引入强凸性,如之前所说,自然是为了更好地榨干函数的价值。这个 $\alpha$ 和 之前的 $\beta$,都是包含了部分二阶信息,再引入 condition number $\kappa = \frac{\beta}{\alpha}$,则可以代表其 Hessian 矩阵至多有多少个特征根。引入强凸性的概念后,如果使 $\eta = \frac{\beta + \alpha}{2}$,那么向最优点的逼近可以达到与迭代次数呈指数级别的速度!
Let $f$ be $\beta$-smooth and $\alpha$-strongly convex on $\mathbb{R}^n$. Then gradient descent with $\eta = \frac{\beta + \alpha}{2}$ satisfies $$f(x_{t+1})-f(x^\ast)\leq \frac{\beta}{2}\exp(-\frac{4t}{\kappa+1})||x_1-x^\ast||^2.$$
Lower Bound
这么一大段东西,其实看个结论就行了。作者写这些的目的,就在于证明在函数各种情形下的理论下界,然后说明,在光滑/光滑+强凸的情况下,结合 凸优化(一) 开头的那张表,可以看出,Lower Bound 仍然和 之前提到的算法的最优复杂度 有差距。有可能逼近到理论下界吗?居然是有的!使用 NAG (Nesterov’s Accelerated Gradient Descent) 或者 下一节的 Geometric Descent Method 就可以做到。
Geometric Descent Method
这个方法的一作就是这篇 monograph 的作者本人,可以说是私货了。不看也行,不过挺有趣的,理解之后也会觉得挺形象,就在这里讲讲。其实光看这一小节,会感觉云里雾里,不如结合原来他的 那篇论文 看。另,共同发明人 Yin Tat Lee 在网上有一个 Lecture Notes,非常助于理解。我就照着 Notes 里的思路来说。
之前我们在讲 椭圆方法) 的时候,也说过,椭圆方法的原理是找出一个分割最优点所在半球和另一个半球的超平面。这样,每次分割一半,再形成包围剩下的那个半球的新椭圆体,从而迭代进行。
但是,Yin Tat Lee 想到,这样是不是有点浪费?他觉得,能够割掉的部分,绝不止是当前体积的 $\frac{1}{2}$,如果能够割更多,那么就能提高指数的基数。此外,比起椭圆方法, Geometric Descent Method 是 dimension-free 的,意味着可以 $t\ll n$,这是在实践中的优点。
Geometric Descent Method 基于以下几点事实:
- 最优点必然在可以处于两个球体的相交处。
- 这个相交处可以被一个新的球体包围。
- 这个新球体的体积比原来的两个球体小,或者一样。
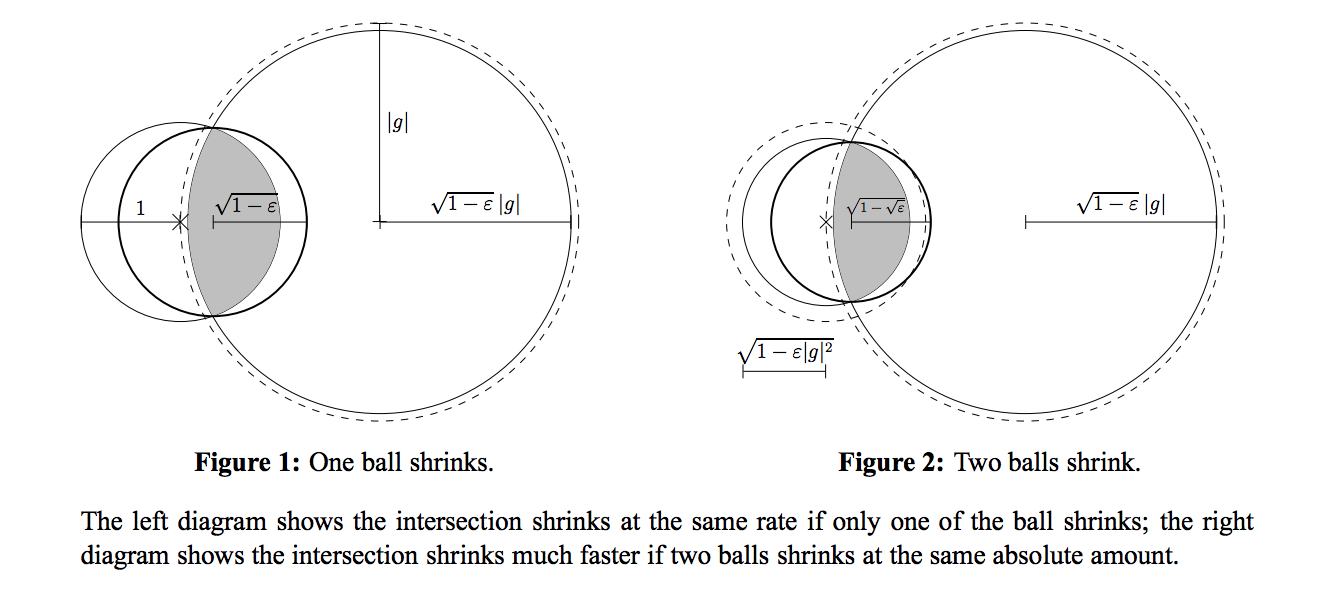
在图中,被虚线包围的两个球体,相交,得到新的迭代的球体。之所以有两幅图,是因为左图可以使用梯度信息,缩小原有的左边的圆(左边的圆是上一次迭代得到的圆),从而加速了球体体积的缩小。
此外,两个球体中的一个球体,可以被另一个球体表达:
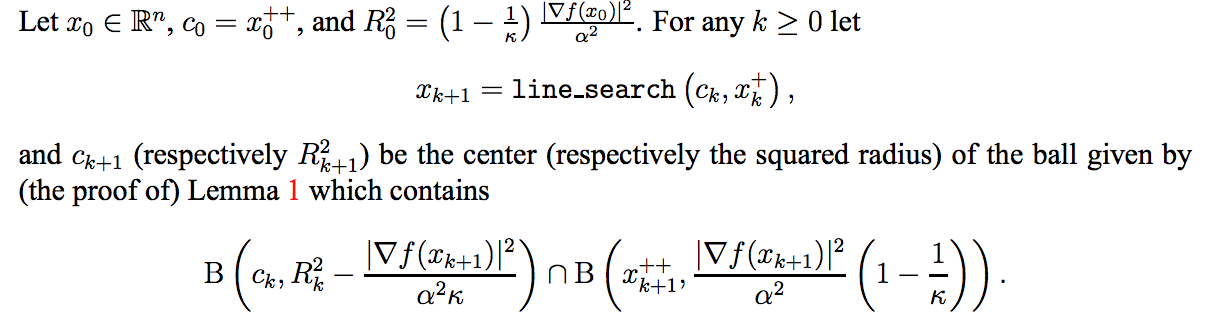
其中,$c_k$ 为第 $k$ 次迭代时的球体圆心,之所以要用 $x_{k+1}$ 而不直接使用 $c_k$ 的原因,在于需要保证 $f(x_{k+1})\leq f(x_{k}^+)$,而我们是不能保证 $f(c_{k+1})\leq f(x_{k}^+)$ 的。因此,使用了 line-search,找到一个满足 $f(x_{k+1})\leq f(x_{k}^+)$ 的点,代替 $c_k$ 计算 $x_{k+1}^{++}$.
另一种看法
虽然说是两个球体,但其中一个球体的半径、球心,是可以被另一个球的信息表达的,因此 Geometric Descent Method 其实是椭圆方法的一个超级衍生物:椭圆方法中的超平面,改为了 Geometric Descent Method 中的二次曲面,这个二次曲面,由被表达的球体组成。因此,它的思想源头是 Cutting Plane Methods,是很巧妙的转型。
说到 Descent,肯定用到了梯度信息。在哪里?被利用在了生成另一个球体的时候,因此,不再需要每次查询 oracle 当前最佳的超平面,从而实现了 dimension-free。
总结
理解 Geometric Descent Method 花了一些不必要的时间,这种无成效的事,以后少做了。第六天,完成!
第七天
Nesterov’s Accelerated Gradient Descent
好了,它终于来了。
先上算法。
The smooth and strongly convex case ($\kappa=\frac{\beta}{\alpha}$) :$$y_{t+1}=x_t-\frac{1}{\beta}\nabla f(x_t),$$ $$x_{t+1}=(1+\frac{\sqrt{\kappa}-1}{\sqrt{\kappa}+1})y_{t+1}-\frac{\sqrt{\kappa}-1}{\sqrt{\kappa}+1}y_t.$$
The smooth case: $$\lambda_0=0,\text{ }\lambda_{t}=\frac{1+\sqrt{1+4\lambda_{t-1}^2}}{2},\text{ and }\gamma_{t}=\frac{1-\gamma_{t}}{\gamma_{t+1}},$$ $$y_{t+1}=x_t-\frac{1}{\beta}\nabla f(x_t),$$ $$x_{t+1}=(1-\gamma_t)y_{t+1}+\gamma_t y_t$$
无论是 smooth case 还是 smooth and strongly convex case,NAG 都是最优的,完全和 lower bound 在同一个尺度。但关于 NAG 背后的 Intuition,其实一直是一个谜。这么奇奇怪怪的迭代式子,他到底是怎么想出来的?
如果我们单看 smooth case,从结果上逆推,可以看到:
$$x_{t+1}=(1-\gamma_t)y_{t+1}+\gamma_t y_t$$ $$\iff x_{t+1}=y_{t+1}+\gamma_t (y_t-y_{t+1})$$
如果 $\nabla f(x_{t+1})+\gamma_t (\nabla f(x_t)-\nabla f(x_{t+1}))$ 可以近似为 $\nabla f(x_{t+1} + \gamma_t (x_{t}-x_{t+1}))$,那么更新规则可以改写为:$$x_{t+1}=(x_{t+1}+\gamma_t (x_t-x_{t+1})) -\frac{1}{\beta}\nabla f(x_{t+1} + \gamma_t (x_{t}-x_{t+1}))$$
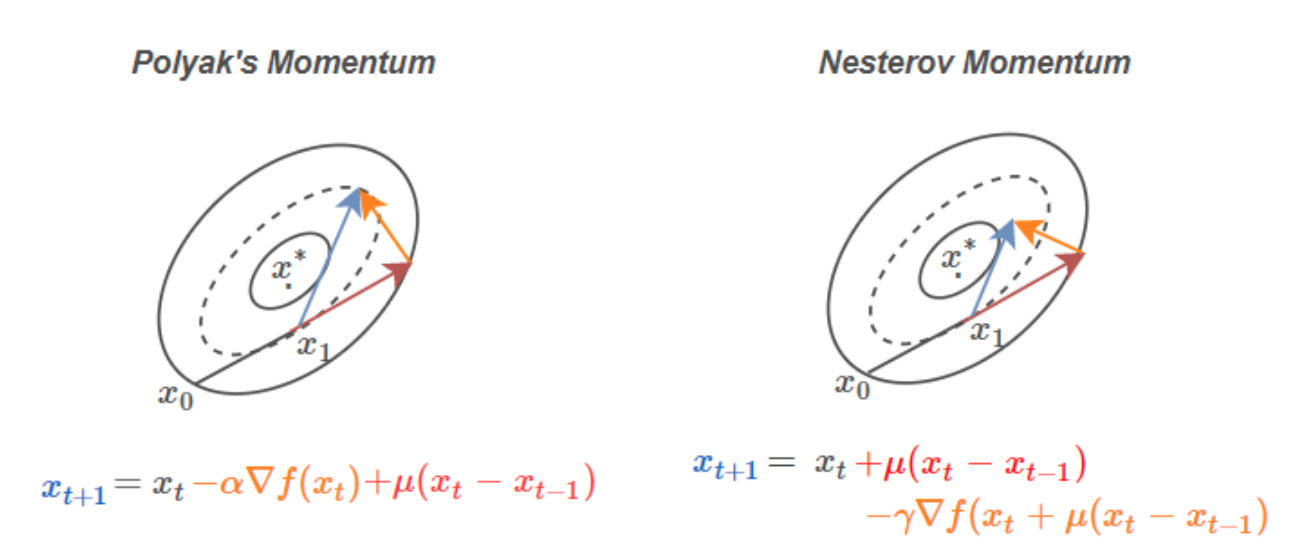
This figure:We see that Polyak’s method evaluates the gradient before adding momentum, while Nesterov’s
algorithm evaluates the gradient after applying momentum.
比起动量算法,Nesterov 提前估计了即将降落的点的梯度。但从收敛性的证明来看的话,自然是变快的。但是,到底为什么会变快呢?目前我在网上没找到比较容易理解的解释。更为形象的一种替代方法,就是上述讲到的几何下降方法,但是其不能用于 smooth case,就有些遗憾。在作者的 Revisiting Nesterov’s Acceleration 博客当中,谈到了 Allan Zhu 的论文,论文将 Nesterov 方法视为镜像下降法和梯度下降法的线性耦合,给出了 nice proof。
用了二阶信息?
一些博文 说 Nesterov 这么快,是因为它用了二阶信息。要这么说也行,毕竟使用了 $\beta$-smooth,即光滑性的一部分结论。
但是,从另一个角度来说,它并没有直接计算二阶导,顶多是估计了 $\beta$,因此也可以说没有利用二阶信息。总而言之,它利用的信息和其他 Gradient Descent 方法是一样的,并没有作弊。
总结
行了,Dimension-free 这章结束了。主要讲了一些梯度方法,迭代次数可以远远小于维数。完!
第八天
Mirror Descent
看镜像下降法的同时,由于不太能够理解背后的原理,去找了一下相关的资料,顺藤摸瓜,找到了朱泽园的一段 Talk,感觉醍醐灌顶,大局观瞬间清晰了起来,传了若干年的功力。建议大家都看一看这个思路:
言归正传。为什么会有 Mirror Descent?因为有的约束集所在的空间很特殊,不能使用普通的欧几里得度量进行距离的计算。在这种情形下,$x-\eta \nabla f(x)$ 是没有任何意义的,因为数值上的减法在这个空间中不适用。比如,定义域为 ${x: \sum_{i=1}^n x_i = 1}$。这个时候该怎么办?
思路就像下图一样,先将 $x_t$ 映射至 $\nabla \Phi (x_t)$,在使用可以在 $\mathbb{R}^n$ 中进行的梯度下降,变为 $\nabla \Phi (y_{t+1})$,将其映射回原空间后,得到 $y_{t+1}$。由于 $y_{t+1}$ 可能并不在原定义域,则再使用投影方法,投影到 $x_{t+1}$。这里的投影函数,使用的是 Bregman Divergence,原因很深奥,可以参考 Mirror descent: 统一框架下的 first order methods,我目前没必要懂,所以不解释。

可以说,Mirror Descent 方法是 Projected Descent 的一个推广,推广的地方是在于原凸集可以不再使用欧几里得度量,而可以是任意度量。我个人认为,它的难点在于,$\Phi$ 很难找,构造起来需要一定的技术。
Lazy
它有一个变体,是在对偶空间中不断地更新点,直到原空间要求得到更新点的时候,再映射回去。这样就省去了很多往返映射的计算。性能上是 $\frac{1}{\sqrt{t}}$,比原 Mirror descent 慢上 $\frac{1}{\sqrt{t}}$.
Mirror Prox
Mirror Descent 的另一个变体叫做 Mirror Prox,它先预测了下一个降落点,再根据下一个降落点的梯度更新当前点。它的迭代速度是 $\frac{1}{t}$,和 Mirror Descent 是一样快的,不过似乎在之后的篇章中会得到版本加强。
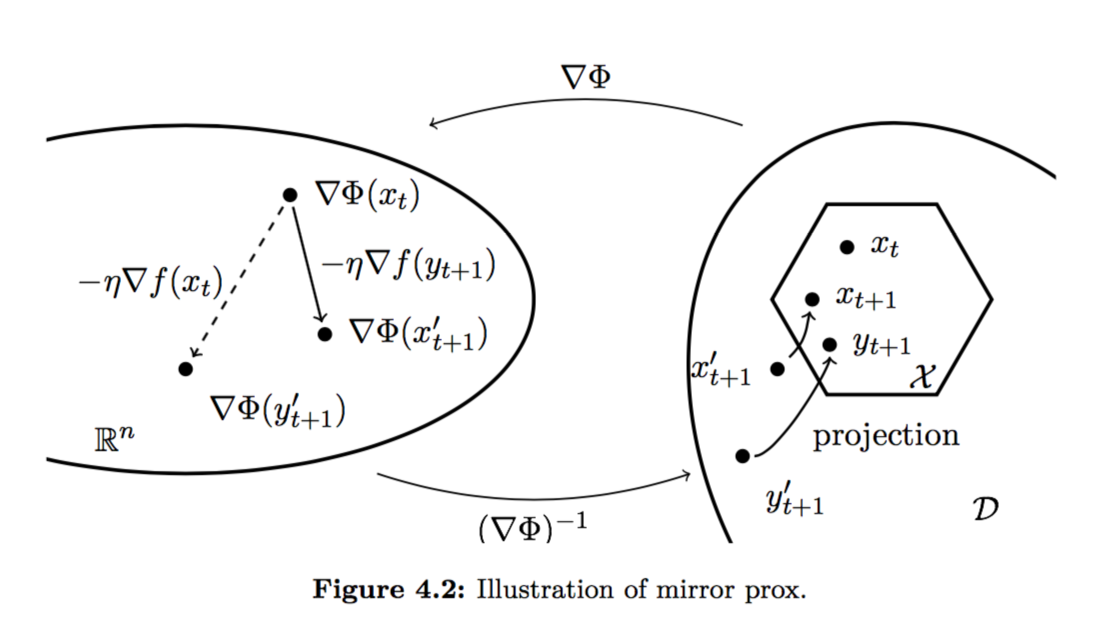
为什么使用 $\nabla \Phi(\cdot)$ 表示映射函数
为什么要加一个 $\nabla$ 呢?后来我发现,这是为了和 Bregman Divergence 的形式保持一致。可以参见 如何理解Bregman divergence? 中的这张表:

总结
今天看得很快,主要是有其他文章的指导,站在了巨人的肩膀上。第八天,解!
说明
如未说明,则图均出自 Convex Optimization: Algorithms and Complexity。